Im folgenden beschreibe ich einige meiner Erfahrungen mit dem Carbon-Tinten-Druck. Eine ausführlichere Darstellung samt den mathematischen Details kann man als pdf-Datei unter www.kuhlmann.at/download/photography herunterladen.

Eine interessante Eigenschaft von Pigment-Druckertinten

Bei der Kalibrierung eines Tintensatzes für die Verwendung mit Quad Tone Rip (QTR) muss man einen Teststreifen mit 21 oder 51 Graustufen drucken und ausmessen, wobei die K-Werte gleichmäßig zwischen 0 und 100 verteilt sind (K steht für den Bedeckungsgrad des Papiers mit reinem Schwarz). Dabei fiel mir eine interessante Eigenschaft auf, die vermutlich den Fachleuten gut bekannt ist, die ich aber in keiner Anleitung oder Diskussion zu QTR gefunden habe: Die Luminanz L (visuelle Helligkeit, das Sternchen habe ich der Einfachheit halber weggelassen) einer Tinte in Abhängigkeit von der auf das Papier aufgetragenen Tintenmenge nimmt in guter Näherung exponentiell mit K ab. Damit dies zutrifft, sollte die Tröpfchengröße der Tinte konstant sein. Deshalb verwende ich in QTR die höchstmögliche Druckauflösung. Dieselbe funktionale Abhängigkeit wurde bereits vor über 150 Jahren für die Abschwächung der Intensität elektromagnetischer Strahlung beim Durchgang durch ein absorbierendes Medium entdeckt. In der Physik ist diese Beziehung als Beer-Lambert-Gesetz bekannt.

Beim Drucken wollen wir jedoch keine exponentielle Abnahme der Luminanz in Abhängigkeit von der Tintenmenge, sondern eine lineare Abnahme von L mit K! Wenn man die exponentiell abfallende Funktion kennt, kann man jedoch eine mathematische Transformation der Luminanzfunktion vornehmen, um die Tintenmenge vorherzusagen, die notwendig ist, damit die Luminanz des gedruckten Targets linear von K abhängt. Wenn es keine Fehlerquellen gäbe und die Abhängigkeit L(K) exakt durch eine mathematische Formel beschrieben werden könnte, wäre es möglich, eine Quad-Datei zu erstellen, die genau linear druckt. Idealerweise bräuchte man dann weder ein Ausprobieren der Mengen und des K-Bereichs für einzelne Tinten im QTR Curve Tool noch eine nachträgliche Linearisierung.

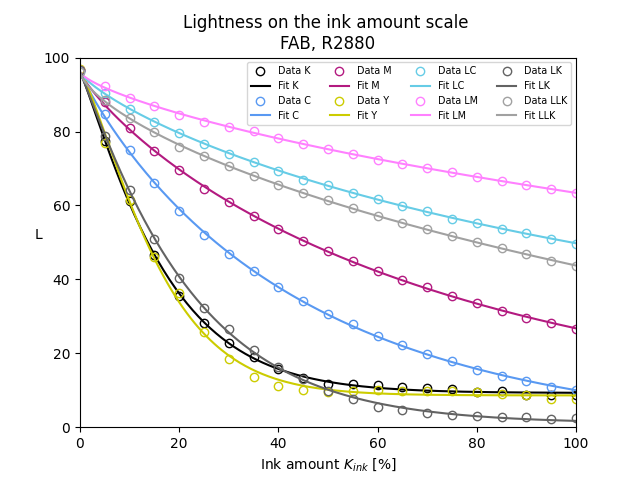
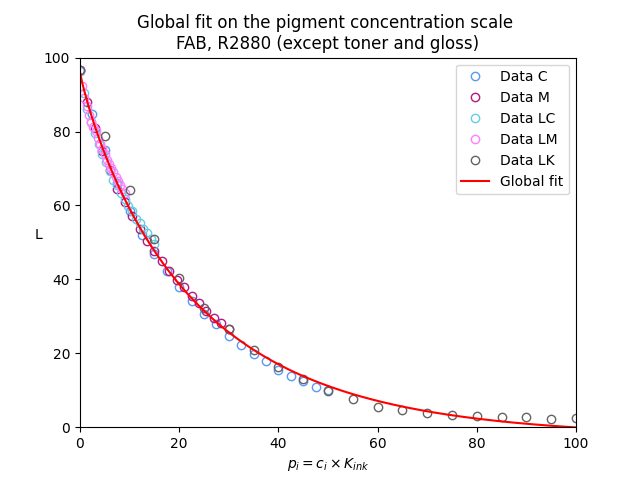
In der Realität ist es allerdings etwas komplizierter: Die Abhängigkeit L(K) ist nicht exakt exponentiell, lässt sich aber sehr genau durch leicht modifizierte Funktionen approximieren. Die Luminanzfunktionen hängen zudem vom Papier und dessen Oberflächenstruktur ab. Außerdem ist die Luminanz, die mein Epson R2880 druckt, nicht immer exakt reproduzierbar, und auch das Messgerät (ColorMunki Photo) hat eine gewisse Ungenauigkeit. Dennoch hat dieser Ansatz für mich gut funktioniert. Abbildung 1 zeigt ein Beispiel für Hahnemühle FineArt Baryta und den GCVT-Tintensatz von Paul Roark mit einem 21-stufigen Graukeil. Durch Skalierung der L(K)-Daten für die einzelnen Tinten mit der Pigmentkonzentration c_i lassen sich alle Luminanzkurven annähernd zur Deckung bringen (Abb. 1b).

Erstellen von Quad-Dateien

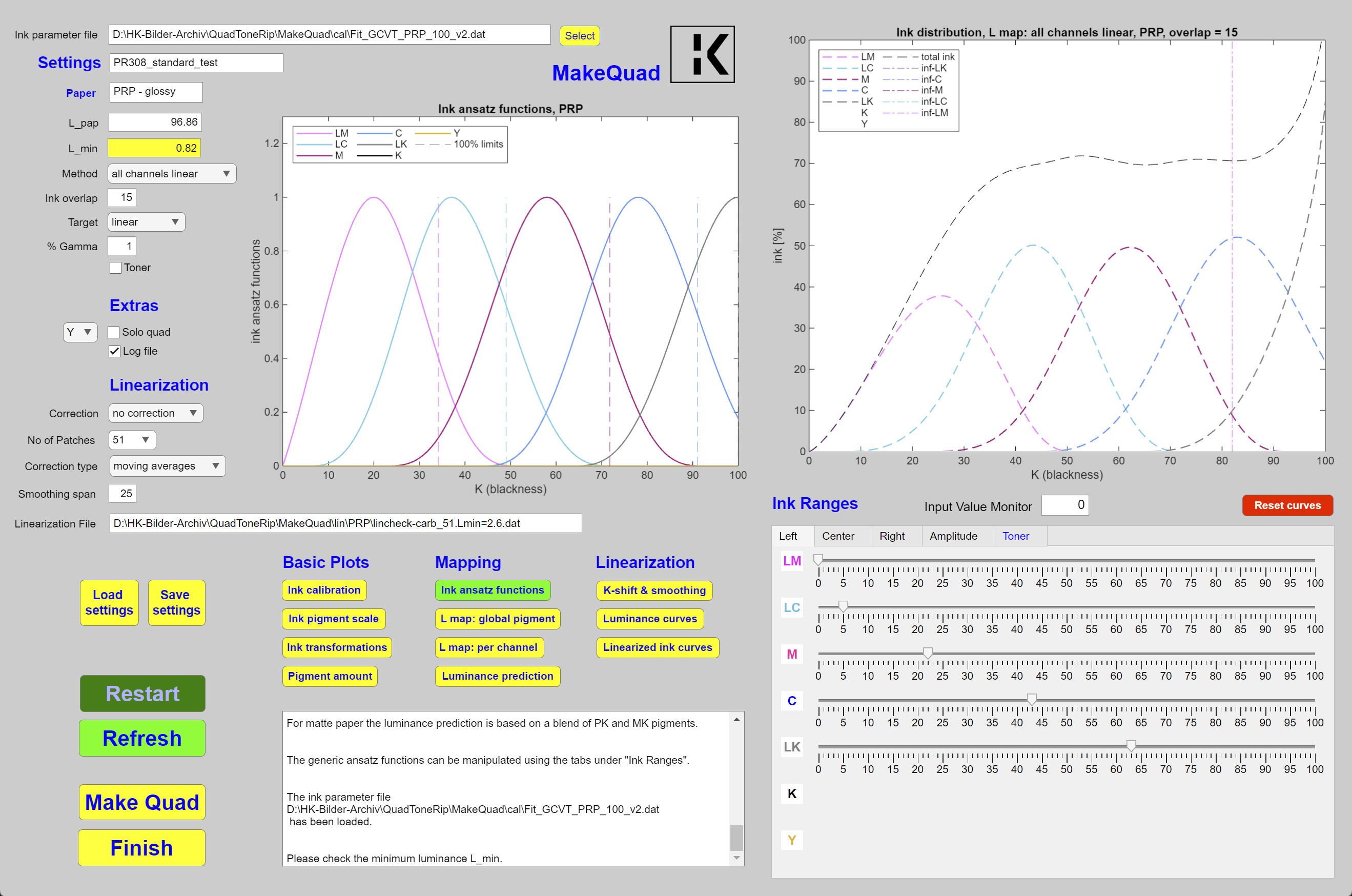
Die oben beschriebene Eigenschaft der Tinten kann genutzt werden, um die Luminanzfunktion(en) in lineare Funktion(en) umzuwandeln und die Tintenanteile für den Druck zu bestimmen. Dies geschieht mit geeigneten Ansatzfunktionen, die positiv und auf 1 normiert sind. Deren Wichtung bestimmt dann die gedruckte Tintenmenge als Funktion von K. Um glatte Ansatz-Funktionen zu erhalten, verwende ich kubische Hermite-Splines, die zur Potenz 1.7 erhoben wurden, was die Ansatzfunktionen etwas schlanker als die ursprünglichen kubischen Hermite-Splines macht. Diese Funktionen sind sehr ähnlich (fast identisch) zu den Kurven des Piezography-Systems. Ein Beispiel für die Ansatzfunktionen ist im linken Diagramm von Abbildung 2 zu sehen. Die Abbildung zeigt die Benutzeroberfläche unter Windows 11, die ich derzeit programmiere, um Quad-Dateien basierend auf diesem Ansatz zu erstellen, die dann mit QTR zum Drucken verwendet werden können. Ein wichtiger Parameter ist der Überlappungsbereich der Ansatzfunktionen. Es kann vorkommen, dass die Luminanz bei der Messung der 21-Stufen-Testreihe zwar perfekt linear erscheint, aber beim Drucken eines „Bull’s Eye“-Musters erkennt man, dass die Übergänge zwischen den Tinten nicht glatt genug sind. In diesem Fall kann eine Vergrößerung der Überlappung das Problem lösen. Neben einem globalen Überlappungsparameter in der GUI kann derzeit auch der Bereich jeder Ansatzfunktion (linker und rechter Punkt) sowie die Lage des Maximums (Mittelpunkt) für jede Tinte eingestellt werden. Das Programm aktualisiert dann alle Tintenfunktionen (rechtes Fenster) so, dass das gedruckte Ergebnis linear ist – bis auf die oben genannten Fehlerquellen.

Glänzend und matt drucken

Derzeit verwende ich den GCVT-Tintensatz von Paul Roark. Dieses Tintenset besteht im Wesentlichen aus glänzenden Tinten auf PK-Basis, wobei ein Kanal mit matter schwarzer Tinte (MK) belegt ist (auch der Y-Kanal). Diese Konfiguration erlaubt das Drucken sowohl auf glänzenden als auch matten Papieren. Beim Drucken auf glänzendem Papier werden nur Tinten verwendet, die Verdünnungen derselben schwarzen PK-Tinte sind. Wie oben gezeigt, lassen sich die Luminanzfunktionen aller Verdünnungen durch einfache Skalierung von K (entsprechend der PK-Konzentration) auf eine gemeinsame Kurve abbilden – das nenne ich Pigment-Mapping. Diese Zuordnung ist die Standardeinstellung in der GUI (siehe Abbildung 2).

Beim Drucken auf mattem Papier muss der MK-Kanal für die dunkelsten Töne verwendet werden, da PK auf mattem Papier kein echtes Schwarz erreicht. Auf mattem Papier sättigt die Luminanz der PK-Tinte bereits bei K ≈ 93. Daher kann keine einfache Skalierung von K gefunden werden, um alle Luminanzkurven auf eine gemeinsame Master-Kurve zu bringen. Das wäre nur möglich, wenn alle Grautinten für matte Papiere Verdünnungen derselben MK-Tinte wären. Dies ist der Preis für die Flexibilität, sowohl auf glänzendem als auch mattem Papier drucken zu können. In diesem Fall können die Kanäle individuell linearisiert und dann gemäß den Ansatzfunktionen kombiniert werden. Dabei ergeben sich leider Einschränkungen: Helle Tinten können nicht die dunkelsten Töne drucken, deshalb divergiert die benötigte berechnete Tintenmenge bei charakteristischen K-Werten. Die PK-basierten Tinten (alle außer MK) sollten daher nur bis zu einem bestimmten K-Wert eingesetzt werden, insbesondere der PK-Kanal darf beim Linearisieren nicht bis K=100 verwendet werden. Die tiefsten Töne (K > 93) müssen ausschließlich mit MK gedruckt werden. Theoretisch könnte dies in den tiefsten Schattenbereichen eine leichte Körnigkeit verursachen, doch unter normalen Betrachtungsbedingungen ist dies kaum sichtbar. Wenn man PK bis K=100 nutzen will, muss man auf die automatische Linearität verzichten und einen anderen Ansatz wählen. Eine Alternative wäre, den Y-Kanal (der ursprünglich ebenfalls mit MK Tinte gefüllt ist und für das Drucken auf Arches Aquarellpapier benötigt wird) mit leicht verdünnter MK-Tinte zu laden – möglicherweise gar keine schlechte Idee.

Luminanzvorhersage

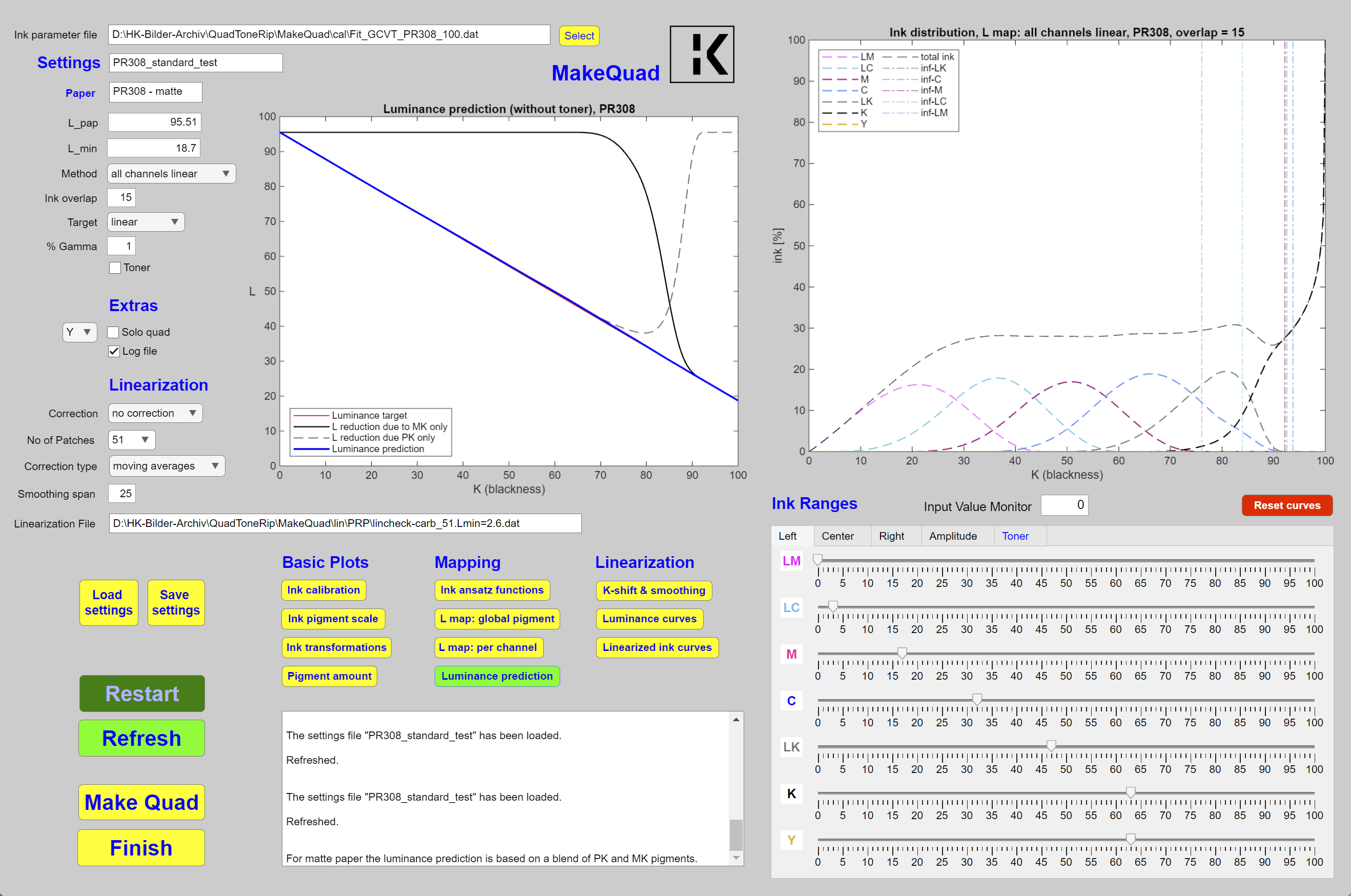
Wenn man die automatische Linearisierung aufgibt, um die PK Tinten auf der vollen K-Skala zu verwenden und die Tinten frei kombiniert, dann erhebt sich die Frage: Wie soll man denn kombinieren? Um geeignete Tintenverteilungsfunktionen zu finden, verwende ich eine Vorhersage der Luminanz. Sie basiert auf der Kenntnis des Anteils des Papiers bzw. eines Pixels, das mit Pigment bedeckt ist und so die Luminanz des Papiers reduziert. Wenn man dies herausgefunden und durch die verwendete Tintenmenge ausgedrückt hat, muß man sich nur noch überlegen, wie sich die verschiedenen Tinten (PK, MK und Toner) überlagern. Dann kann man eine Formel für die Luminanzreduktion der Überlagerung dieser Tinten finden. Ich war selbst überrascht, wie gut diese Vorhersage funktioniert, nicht nur für den Fall eines reinen Carbondrucks auf glänzendem Papier (mit nur einer Sorte von Pigment), sondern auch für neutralisierte Tintenverteilungen auf mattem Papier (3 Sorten von Pigment). Ein Beispiel für die Luminanzvorhersage für eine linearisierte Tintenverteilung ist in Abb. 3 für zwei Pigmente (MK und PK) gezeigt. Die Linearität wurde auch im Druck durch Messung bestätigt.

Tonung

Das CGVT-Tintenset enthält einen Blaukanal, der von Paul Roark entwickelt wurde, um den bräunlichen Farbstich der reinen Carbontinten, besonders auf glänzendem Papier, zu neutralisieren. Mir ist keine Theorie bekannt, die eine Korrektur dieses Farbstichs in einem Rutsch erlaubt, so wie beim Pigment-Mapping der Carbontinten. Daher muss der nötige Blauanteil iterativ ermittelt werden, um ein nahezu neutrales Grau über die gesamte K-Skala zu erreichen. Ein Beispiel dafür ist im rechten Diagramm von Abbildung 1 zu sehen. Die blaue Kurve zeigt die Tonermenge für Hahnemühle FineArt Baryta. Der aktuelle Wert wird durch kubische Splines berechnet, basierend auf 11 Kontrollpunkten (Kreise), die über Schieberegler unter der Registerkarte 'Toner' angepasst werden können.

Linearisierung

Es kann vorkommen, dass die angestrebte lineare Kurve durch das Mapping nicht exakt erreicht wird. Dies ist erst recht bei der freien Wahl der Tintenverteilung zu erwarten. Beim Pigment-Mapping kann dies daran liegen, dass die Luminanzkurven leicht vom Durchschnittsfit (rote Linie in Abb. 1b) abweichen. Deshalb ist eine Linearisierung implementiert, ähnlich wie im QTR Curve Tool, basierend auf einer gemessenen Testreihe (Standard: 51 Graustufen, siehe Abb. 2). Dabei kann man verschiedene Glättungsoptionen für die gemessene Abweichung von der Linearität wählen (stückweise linear, Polynome 6. Ordnung, gleitende Mittelwerte), die dann zur Korrektur verwendet wird. Die Standardglättung ist ein gleitender Mittelwert mit einem Fenster von 25 Punkten.

Gamma-Korrektur

Da die exponentiellen Luminanzfunktionen in lineare umgewandelt werden können, lassen sie sich auch in jede andere gewünschte Luminanzkurve transformieren – vorausgesetzt, diese ist streng monoton (bijektiv). Da die lineare Kurve oft zu helle Schatten ergibt, sollte die Zielkurve leicht von der Linearität abweichen, um einen besseren visuellen Eindruck zu erzielen. Ich nenne das hier eine Gamma-Korrektur, obwohl es sich nicht um eine echte (drastische) Gamma-Kurve handelt, die viel zu dunkle Drucke ergeben würde. Paul Roark hat hierfür eine Photoshop-Korrekturkurve bereitgestellt, mit der modifizierte TIFF-Dateien vorbereitet werden können, die in Photoshop zu dunkel aussehen, aber mit QTR korrekt gedruckt werden. In meiner derzeitigen Methode wird die Gamma-Korrektur direkt in die Quad-Datei eingeschrieben. Dafür habe ich eine 21-stufige Testreihe gemessen, die mit dem Epson-Treiber des P900 und Standard-Einstellungen gedruckt wurde. Die Luminanzdaten wurden dann mit kubischen Splines interpoliert und im Code implementiert. Die GUI erlaubt es zudem, den Gamma-Korrekturanteil über einen Gewichtungsfaktor zwischen 0 und 1 zu steuern. Es wäre auch einfach, beliebige andere bijektive Zielkurven zu implementieren – zum Beispiel für die Erstellung von Negativen für alternative fotografische Prozesse.

Im Juni 2025